Knight dialer #

Description #

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

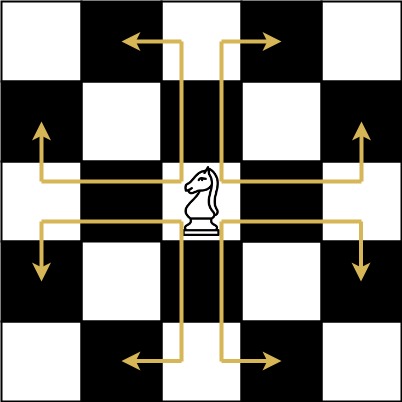
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

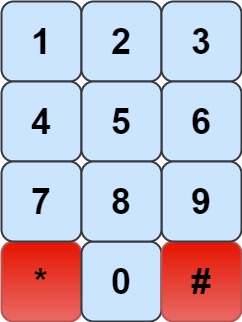
Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially
and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo \(10^9 + 7\)

Example 1:

Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient

Example 2:

Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod

Constraints:

• 1 <= n <= 5000

Solution #

High level #

• Có thể thấy bàn phím điện thoại khá nhỏ
• Ta có thể tận dụng các giới hạn này để giải quyết bài toán thay vì đâm đầu vào một công thức tổng quát:
  • Ở một vị trí chỉ có thể nhảy đến 1 tập giới hạn các vị trí khác
  • Số cách di chuyển ở mỗi vị trí là hằng số và có thể liệt kê được

Low level #

Ta nên bắt đầu bằng 1 ví dụ: đẹp nhất là n = 3

• Ở lần đầu thì vị trí là tất cả các nút
• Ở lần 2 thì cần duyệt qua từ 0 đến 9
  • vị trí 0 sẽ có thể nhảy đến 4 và
  • vị trí 1 sẽ có thể nhảy đến 8 và
  • …
• Ở lần 3 thì
  • ta sẽ duyệt tiếp bên trong vị trí 0 ở lần 2
    • vị trí 4 sẽ có thể nhảy đến 3, 9 và 0
    • vị trí 6 sẽ có thể nhảy đến 1, 7 và 0
  • trong vị trí 1 ở lần 2
    • 8 => 1, 3
    • 6 => 1, 7, 0
  • …

Các kết quả cần tìm

• Với n = 1, return 10
• Với n = 2,
  • 0 có thể đến 4 và 6,
  • 1 có thể đến 8 và 6
• Với n = 3,
  • 0 có thể đến 3, 9, 0, 1, 7, 0
  • 1 có thể đến 1, 3, 1, 7, 0

Kết quả là tổng sống lượng vị trí có thể đến

• Cần tạo 1 mảng chứa các vị trí khả dụng qua mỗi lần lặp n

Có thể thấy ta có thể tạo 2 mảng

• Mảng số vị trí khả dụng kế tiếp khi ở vị trí i: [[4, 6], [8, 6], []]
• Có thể thấy để dùng được mảng vị trí khả dụng thì n phải >= 2
• Vậy thì thuật toán cần tìm phải bắt đầu ít nhất từ 2

/**
 * @param {number} n
 * @return {number}
 */
var knightDialer = function (n) {
  const nextPlaces = [
    [4, 6],
    [6, 8],
    [7, 9],
    [4, 8],
    [0, 3, 9],
    [],
    [0, 1, 7],
    [2, 6],
    [1, 3],
    [2, 4],
  ];

  if (n === 1) return 10;

  const validPlaces = JSON.parse(JSON.stringify(nextPlaces));
  for (let time = 3; time <= n; time++) {
    for (let place = 0; place <= 9; place++) {
      const newPlaces = [];
      for (let i = 0; i < validPlaces[place].length; i++) {
        newPlaces.push(...nextPlaces[validPlaces[place][i]]);
      }
      validPlaces[place] = newPlaces;
    }
  }
  const totalWays =
    validPlaces.reduce((acc, currentArray) => acc + currentArray.length, 0) %
    (Math.pow(10, 9) + 7);
  return totalWays;
};

Xuất hiện lỗi runtime error: Cụ thể thì là do out of memory

• Khi thử với các test case nhỏ thì dễ thấy hàm của chúng ta work như mong đợi
• Nhưng khi thử với số lớn thì sẽ xuất hiện lỗi out of memory
  • Giải thuật chưa tối ưu bộ nhớ ?
  • Chọn cấu trúc dữ liệu chưa phù hợp ?

Optimize #

Retrospective #

Cùng nhìn lại cách diễn giải ban đầu:

• n = 1: tất cả các nút
  ==> [[0], [1], [2], [3], [4], [5], [6], [7], [8], [9]]
• n = 2:
  • 0 có thể đến 4 và 6
  • 1 có thể đến 8 và 6
  • 2 có thể đến 7 và 9
  • …
    ==> [[4, 6], [6, 8], [7, 9], [4, 8], [0, 3, 9], [], [0, 1, 7], [2, 6], [1, 3], [2, 4]]
• n = 3:
  • 0 có thể đến 3, 9, 0, 1, 7, 0
  • 1 có thể đến 1, 3, 1, 7, 0
  • …
    ==> [[3, 9, 0, 1, 7, 0], [1, 3, 1, 7, 0], ...]
• …

• Dễ thấy n càng cao số phần từ trùng lặp lại trong mảng càng cao
• Với mỗi phần tử trùng ấy ta lại có cùng một công việc cho chúng
• Kết quả cần tìm lại là đếm số lượng phần tử của từng mảng

==> Nếu có thể áp dụng cấu trúc Dictionary sẽ là một phương pháp tối ưu

New way #

Cách diễn dãi mới

• n = 1
  ==> dic = {0: 1, 1: 1, 2: 1, 3: 1, 4: 1, 5: 1, 6: 1, 7: 1, 8: 1, 9: 1}
  ==> dic = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
  ==> Nên chọn array vì key chúng ta cần chỉ là các con số từ 0->9
• n = 2
  • 0 có thể đến 4 và 6 => newDic[4] += dic[0] và newDic[6] += dic[0]
    • newDic[4] += dic[0] vì giả sử vị trí 0 đang chứa 2 khả năng, thì 2 khả năng đó đều đi đến được 4
    • Dùng newDic là để trạng thái cũ k bị xáo trộn khi đang duyệt
  • 1 có thể đến 8 và 6 => newDic[8] += dic[1] và newDic[6] += dic[1]
  • …

/**
 * @param {number} n
 * @return {number}
 */
var knightDialer = function (n) {
  const nextPlaces = [
    [4, 6],
    [6, 8],
    [7, 9],
    [4, 8],
    [0, 3, 9],
    [],
    [0, 1, 7],
    [2, 6],
    [1, 3],
    [2, 4],
  ];

  if (n === 1) return 10;

  let dic = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1];

  for (let time = 2; time <= n; time++) {
    const newDic = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
    for (let place = 0; place <= 9; place++) {
      for (let i = 0; i < nextPlaces[place].length; i++) {
        newDic[nextPlaces[place][i]] += dic[place] % (Math.pow(10, 9) + 7);
      }
    }
    dic = newDic;
  }
  const totalWays =
    dic.reduce((acc, item) => acc + item, 0) % (Math.pow(10, 9) + 7);
  return totalWays;
};

Time and space complexity optimize #

/**
 * @param {number} n
 * @return {number}
 */
var knightDialer = function (n) {
  const nextPlaces = [
    [4, 6],
    [6, 8],
    [7, 9],
    [4, 8],
    [0, 3, 9],
    [],
    [0, 1, 7],
    [2, 6],
    [1, 3],
    [2, 4],
  ];

  if (n === 1) return 10;

  const mod = Math.pow(10, 9) + 7;

  let dic = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    newDic = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    place,
    i;

  for (let time = 2; time <= n; time++) {
    newDic = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
    for (place = 0; place <= 9; place++) {
      if (place === 5) continue;
      for (i = 0; i < nextPlaces[place].length; i++) {
        newDic[nextPlaces[place][i]] += dic[place] % mod;
      }
    }
    dic = newDic;
  }
  const totalWays = dic.reduce((acc, item) => acc + item, 0) % mod;
  return totalWays;
};

Reference #

• Leetcode: knight dialer